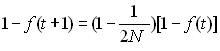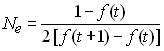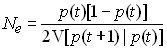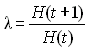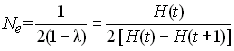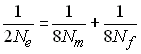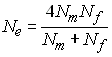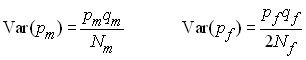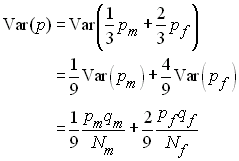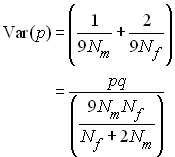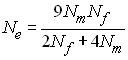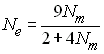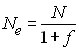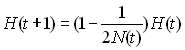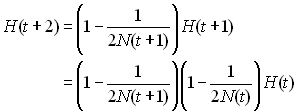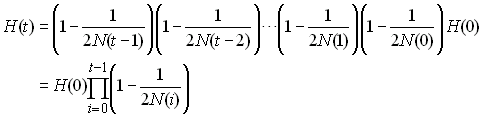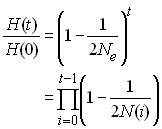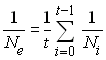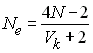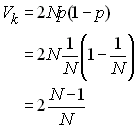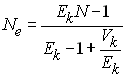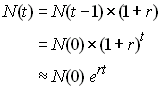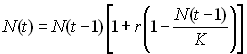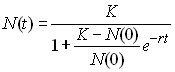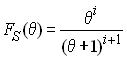Génétique des
populations appliquée aux données moléculaires
| Cours I |
Cours II |
Cours III |
Cours IV |
Cours V |
Cours VI |
Dans les populations naturelles, tous les individus ne
participent pas forcément au processus reproductif, si bien
qu'en général l'effectif de la population N qui
détermine le rythme de la dérive génétique n'est pas égale à l'effectif de recensement de la population. On défini donc
l'effectif
efficace de la population (ou taille
efficace) comme l'effectif d'une population
idéale (de type Wright-Fisher) pour laquelle on
aurait une fluctuation du polymorphisme équivalente à celle de
la population naturelle.C'est donc le
nombre d'individus d'une population idéale pour lequel on aurait
un degré de dérive génétique équivalent à celui de la
population réelle. On note ce nombre comme Ne.
Il y a en fait plusieurs types d'effectif efficace,
selon à quel effet de la dérive génétique on s'intéresse.
Changement de la consanguinité de la population (inbreeding effective population size).
Dans une population idéale, on a vu que la probabilité
que 2 gènes soient identiques par ascendance à la
génération précédente était égal à 1/(2N) et
que le changement du coefficient de consaguinité d'une
génération à l'autre était donné par
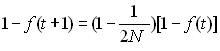
Donc, dans une population réelle, l'effectif efficace sera
celui qui provoquera un changement de
consanguinité de même amplitude que dans une population
idéale.
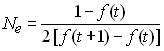
Variance du changement des fréquences alléliques
d'une génération à l'autre (variance
effective population size).
Dans une popualtion idéale, on a vu que la variance de la
fréquence allélique (V(t+1)) conditionnelle à celle de la
génération précédente (p(t)) était donnée par la
variance binomiale
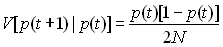
Donc l'effectif efficace de variance sera
donné par quelque chose de la forme
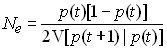
Changement de l'hétérozygotie de la population
d'une génération à l'autre (eigenvalue
effective population size)
Dans une population idéale, on a vu que le changement
d'hétérozygotie d'une génération à l'autre était donné
par le rapport
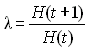
qui était égal à
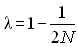
Si bien que l'effectif efficace d'une population réelle
provoquant le même changement d'hétérozygotie que dans une
population idéale sera défini comme
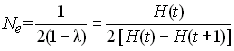
De manière générale, (mais pas toujours) les trois types de
taille efficace donnet des valeurs identiques. On utilisera une
définition ou une autre selon les cas.
1.1 Population avec sexes séparés (dioécie)
Contrairement au modèle de Wright-Fisher, dans une population
avec des sexes séparés deux gènes ne peuvent être identiques
par ascendance (ibd) que 2 générations auparavant.
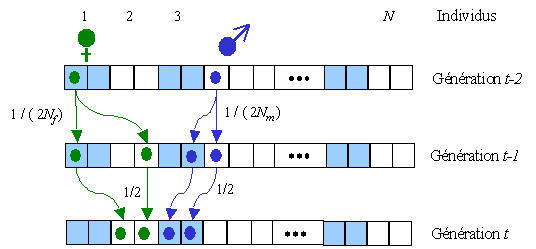
Si l'on considère un individu quelconque, il peut avoir 2
gènes ibd venant de son grand-père ou de sa grand-mère.
Considérons qu'il y a Nm mâles
dans la population et Nf femelles.
Les parents d'un individu de la génération t
peuvent avoir 2 gènes ibd venant d'un mâle (le grand-père)
avec une probabilité 1/(2Nm) (en
bleu sur la figure ci-dessus). Chaque parent a une probabilité
1/2 de lui transmettre son gène ibd, et donc une probabilité
totale de 1/4 que les deux gènes ibd de ses parents lui soient
transmis. Il y a donc une probabilité de 1/(8Nm)
pour que ses deux gènes soient ibd en provenance de son
grand-père. Par le même raisonnement, il y a une probabilité
de 1/(8Nf) pour que ses 2 gènes
soient ibd en provenance de sa grand-mère. Il y a donc une
probabilité totale de 1/(8Nm) +
1/(8Nf) pour qu'il ait 2 gènes ibd.
Or on a vu précédemment que la probabilité qu'un individu
d'une population idéale ait 2 gènes ibd était de 1(2N).
Il en découle que l'effectif efficace de consanguinité
dans une population avec sexe séparé est obtenu en résolvant
l'équation
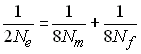
ce qui donne (p. ex. Kimura and Crow 1963)
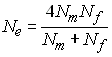
dans le cas ou Nf =Nm
, on a bien Ne = N, mais
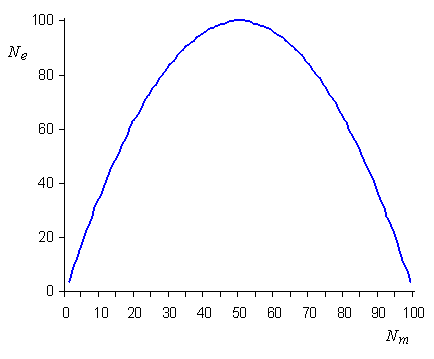
lorsque l'on a des nombres de mâles et de femelles différents
dans une population, l'effectif efficace de la population va être
considérablement réduit, avec un minimum d'environ 4.
Taille efficace
en fonction du nombre de mâles dans la population
|
 |
1.2 Gènes liés au sexes, espèces haplo-diploides
Pour les gènes portés sur le chromosome X ou les espèces
haplo-diploides (p. ex. les insectes sociaux), le calcul de l'effectif efficace est un peu différent que pour les espèces à
sexes séparés. Là on va utiliser l'effectif efficace de
variance, car la notion de consanguinité ne marche pas pour
les haploides.
Une population haplo-diploide est généralement composée de
mâles haploides et de femelles diploides. Considérons un locus
à 2 allèles où la fréquence de l'allèle A est de pm
chez les mâles et pf chez les femelles,
et celle de l'alèle a de qm et qf
chez les mâles et les femelle, respectivement. La variance
d'échantillonnage chez les mâles et les femelles sera
respectivement de
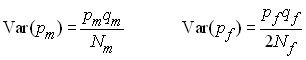
Or la fréquence de l'alèle A dans la population est
donné par
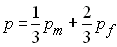
si bien que la variance de p est obtenue
comme
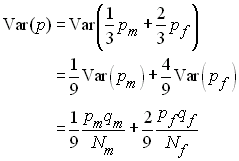
A l'équilibre, pm = pf
= p, et donc
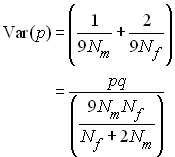
Comme dans une population idéale la variance est
donnée par Var(p) = pq / (2Ne), l'effectif efficace de variance est donnée par
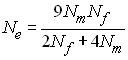
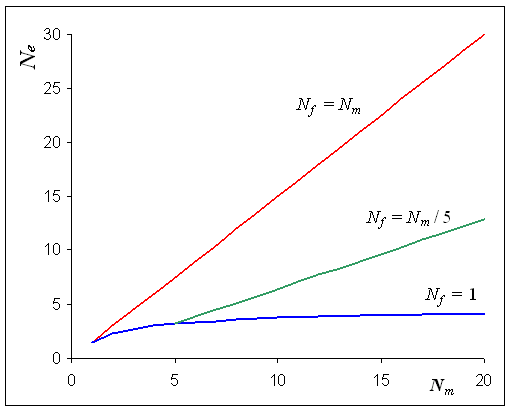
Pour des gènes liés au sexe avec autant de mâles que de
femelles, on a Ne = 2/3 N. Pour
les insectes sociaux qui possède une seule reine qui produit
tous les individus de la population, Nf
= 1 et (Wright 1931)
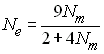
Taille efficace
pour les sytèmes haplo-diploides
|
 |
1.3 Consanguinité
S'il y a de la consanguinité dans la population, l'effectif
efficace de la population sera réduite par un facteur
proportionnel au coefficient de consanguinité
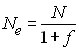
La réduction de taille est donc relativement minime dans les
populations faiblement consanguines. Par contre, chez les plantes
qui ont un fort taux d'autofécondation et où f est
proche de 1, l'effectif efficace peut être seulement la moitié de l'effectif
total.
1.4 Variation de l'effectif de la population au cours du temps
Les populations naturelles sont rarement de taille constante
au cours du temps. Celles-ci puvent en effet fluctuer fortement
de génération en génération, par exemple suite à des
changements climatiques, dans des modèles proies-prédateurs ou
hôtes-parasites, ou encore par l'action de l'homme. Dans ce cas, l'effectif efficace de la population sera proche de la plus petite
taille par laquelle une population a passé au cours de son
histroire récente.
L'effectif efficace dans un tel cas se calcule en fonction de
l'hétérozygotie (Crow et Kimura 1970). On a vu en effet que
dans une population de taille constante
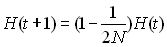
dans une population de taille variable, cette relation sera à
peu près identique, à cela près que l'effectif de la population
sera une variable qui dépendra du temps:
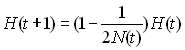
Si l'on étend ce processus sur 2 générations on aura
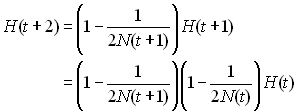
Donc sur un grand nombre de génération on aura quelque chose
de la forme
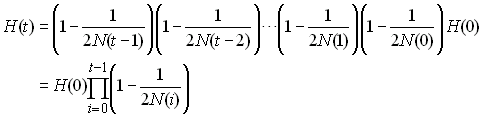
L'effectif efficace de la population sera donc celui d'une
population stationnaire qui causerait la même réduction
d'hétérozygotie après t générations de dérive
génétique, soit
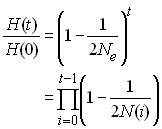
Ceci se résout facilement si l'on fait l'hypothèse que les Ni
sont grands et que l'on utilise l'approximation
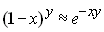 |
si x est petit |
Après résolution, on aura donc
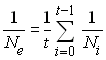
et l'on se rend compte que l'effectif
efficace de valeur propre est
égale à la moyenne harmonique des effectifs précédents de la
population.
On peut appliquer cette formule à différentes situations:
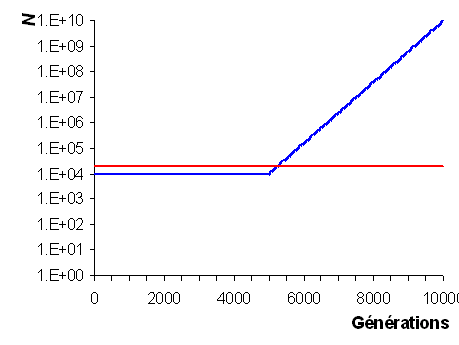
- Effectif efficace de l'espèce humaine:
On fait l'hypothèse que l'espèce humaine a commencé un
cycle de croissance exponentielle il y a 100'000 ans
passant de 10'000 individus à 10 milliards. Avant on
fait l'hypothèse que l'effectif de la population était
constante à 10'000 individus depuis -200'000 ans. En
comptant une génération tous les 20 ans, on arrive à
une moyenne harmonique de 18'648 individus pour les 200
derniers millénaires. Dans ces conditions, on s'attend
donc à ce que la variabilité génétique et
moléculaire de l'espèce humaine soit à peuprès
comparable à celle d'une population idéale d'environ
20'000 individus.
- Bottlenecks périodiques:
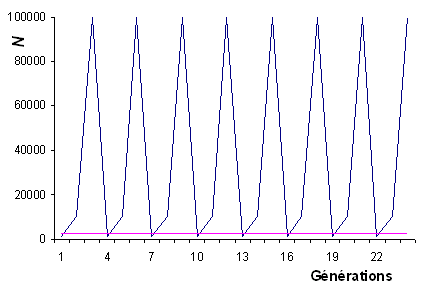
On suppose qu'une population d'insecte décuple sa taille
en 2 générations pendant l'été et qu'ele retourne à
sa taille initiale pendant l'hiver. Elle passera donc par
un cycle de N, 10N et 100N individus
chaque année. Quelle sera sa taille efficace?
Réponse: 2.7N seulement, et pas 36.7 N
comme l'indiquerait la moyenne arithmétique des tailles
de population.
1.5 Structure par âge
Lorsque la population est structurée en classes d'âges, avec
des individus qui ne se reproduisent pas encore ou plus, l'effectif efficace de la population sera
inférieur à l'effectif de
recensement. Dans ce cas il y a plusieurs façons de calculer l'effectif efficace et
Nei et Imaizumi (1966) suggèrent que l'effectif efficace est donné par
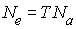
où T est l'âge moyen à la reproduction (le temps de
génération) et Na est le nombre moyen
d'individus nés chaque année qui vont arriver à l'âge de
reproduction. A partir des données démographiques d'Amérique
du Nord, Felsenstein (1971) a calculé que l'effectif efficace
de la population était environ 34% de l'effectif de
recensement, ce qui correspond grossièrement au tiers de la
population, soit à la proportion des gens féconds de la
population.
1.6 Variabilité du nombre de gamètes transmis par individu
Dans le modèle de Wright-Fisher, on fait l'hypothèse que le
nombre de gamètes transmis par individu suit une loi de poisson
de paramètre l=2. Cependant, dans des
populations naturelles de taille constante, le nombre de gamètes
transmis k peut avoir une plus grande variance que celle
d'une loi de Poisson (p. ex dans des population animales avec
harems) ou bien une variance plus petite (p.ex chez des oiseaux
qui contrôlent le nombre d'oeufs par nid). Dans ce cas, l'effectif efficace d'une population de taille constante qui a une
variance Vk du nombre de gamètes
transmis par individu est donné par
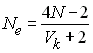
Losqu'il y échantillonnage aléatoire des gamètes d'une
génération à l'autre, la probabilité qu'un certain individu
transmette un de ses gamètes est de p=1/N à
chacun des 2N tirages pour former la génération
suivante. Ce nombre suit exactement un loi binomiale de
paramètre b( p, 2N) que l'on
approxime par une loi de poisson de paramètre l = 2Np =2. La variance du nombre de
gamète transmis par individu selon une loi binomiale est
donc
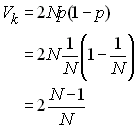
et dans ce cas, l'effectif efficace est donc bien de Ne
= N.
Lorsque l'effectif de la population n'est pas constant, Kimura
et Crow (1963) suggèrent d'utiliser l'expression plus générale
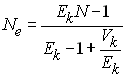
ou Ek est l'espérance du nombre de
gamètes transmis par individu.
Donc d'une manière générale,
- Une variance du nombre de gamètes transmis plus grande
que la moyenne va entraîner une diminution de l'effectif
efficace de la population. ceci revient à dire que la
dérive génétique dans une telle population sera plus
forte que dans une population ou l'espérance et la
variance de k sont identiques.
- Une faible variance du nombre de gamètes transmis peut
paradoxalement conduire à une taille efficace plus
grande que l'effectif de recensement. Ainsi, si Vk
= 0, Ne = 2N-1,
presque le double de l'effectif de recensement. Bien sûr,
ce phénomène indique juste que le rythme de la dérive
génétique est diminué de moitié par rapport à une
population de type Wright-Fisher.
- Dans une population en expansion, le nombre de gamètes
transmis est généralement plus important que dans une
population stationnaire. Mais lorsque l'expansion est
généralisé à tous les membres de la population, la
variance de k est souvent faible et dans ce cas
aussi, on a une taille efficace plus grande que l'effectif
de recensement. Donc pendant des périodes de croissance
de population, on a une réduction de la dérive
génétique dans la population.
Exemples:
- Chez l'homme, Crow et Morton (1955) ont trouvé que l'effectif efficace était
réduit de 5 à 30% selon les
populations de part la grande variance du nombre de
gamètes transmis.
- Dans une population humaine polygame ou la variance du
nombre d'enfants par individus serait 2 fois plus grande
chez les hommes que chez les femmes, soit Vkm
= 4 et Vkf = 2,
on s'attendrait à avoir une taille efficace pour l'ADNmt
qui soit d'environ N/2, mais seulement de N/3
pour le chromosome Y.
2. Modèles démographiques de changement de taille de
population
Les populations naturelles sont rarement stationnaires et
elles peuvent passer par des périodes d'augmentation ou de
réduction d'effectif. Il existe des modèles simples de
croissance de population qui approximent assez bien les
phénomènes réels.
2.1 Croissance ou décroissance exponentielle
On admet que l'on a une population dont l'effectif est augmenté d'un certain facteur r à chaque génération,
soit
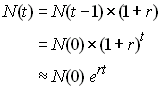
Dans l'exemple de croissance exponentielle de la population
humaine qui aurait passé de 10'000 à 10 milliards d'individus
en 100'000 ans, le facteur d'accroissement r est égal à
0.00276, soit un accroissement de 2.76 pour mille par
génération
De la même manière, on peut avoir une population qui
décroit exponentiellement
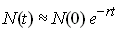
2.2 Croissance logistique
Le modèle de croisance ou décroissance exponentielle n'est
pas toujours réaliste car les conditions de croissance ou
décroissance d'une population vont varier au cours du temps. Par
exemple, des ressources abondantes vont permettre à une
populatin de mieux se nourrir et de croître rapidement, mais au
fur et à mesure de la croissance, chaque individu aura une moins
grande proportion des ressources limitées à disposition. On va
donc introduire la notion de capacité de soutien K
(carrying capacity) d'un
certain environnement, qui exprime l'effectif maximal d'une
population dans un environnement donné. Ainsi, l'évolution de
la population dans un milieu à ressource limité est modélisé
par une croissance logistique de la forme
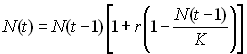
On voit que cela ressemble à de la croissance exponentielle,
mais que le facteur d'accroissement dépend maintenant du rapport de
l'effectif à la génération précédente et de la
capacité de soutien. Le rythme de croissance sera d'autant
plus faible que l'effectif de la popuilation sera proche de la
capacité de soutien. L'équation peut être exprimée en
fonction de N(0) en résolvant une équation
différentielle en approximation continue, ce qui donne
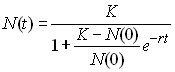
| Croissances
exponentielles et logistiques |
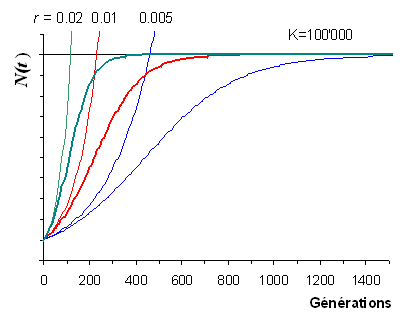 |
On notera que d'autres modèles de croissance logistique ont
été développés, où le fateur d'acroissement est un peu
différent de celui exposé ici.
3. Effet des expansions démographiques sur la diversité
moléculaire
On a vu que la probabilité de coalescence à une génération
donnée dépend de l'effectif de la population, si bien que pour
des populations de taille constante, la longueur des branches
d'une généalogie est directement proportionnelle à l'effectif
de la population (voir différence entre généalogie moyenne pour
des gènes nucléaires et mitochondriaux tirés de la même
population).
Le même raisonnement peut s'appliquer à des populations
de taille variable. Richard Hudson et Montgomery Slatkin
(1991) ont montré que des populations qui étaient entrées en
expansion exponentielle récemment présentaient des arbres en
étoile (star-like trees)
ou en peigne. Alan Rogers et Henry Harpending (1992) on ensuite
montré que des expansions instantanées récentes
étaient de bonnes approximatins de croissances de type
logistiques ou exponentielles. Ces expansions démographiques
laissaient une signature au niveau moléculaire au niveau de la
distribution du nombre de différences par paires. Ces
distributions mismatch présentent en effet une allure unimodale
avec une forme de courbe en cloche.
On peut le comprendre aisément en s'intéressant à la
généalogie d'un échantillon tiré d'une population ayant connu
une croissance démographique récente.
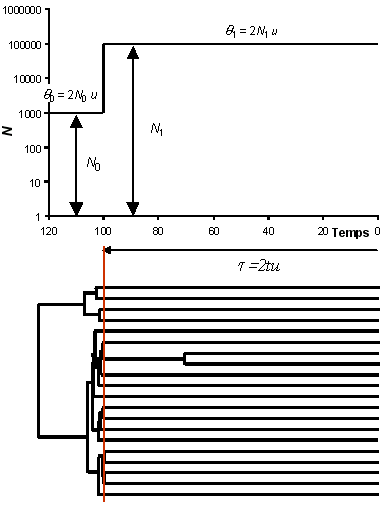
| On représente ici
le profil démographique d'une population ayant eu une augmentation instantanée de taille
d'un facteur 100, passant
d'une taille N0 de 1'000 individus (ici
haploides) à une taille N1 de 100'000
individus. Ceci s'est passé il y a t
générations.
A la génération actuelle, on est donc dans une
grande population, où la probabilité de coalescence
d'une paire de lignage à chaque génération est de 1/ N1.
Comme cette probabilité est petite, les évènements de
coalescence sont rares. Au temps t, la population
passe de N1 à N0 et
la probabilité de coalescence devient 100 fois plus
grande. C'est donc à ce moment que vont se produire la
majorité des coalescences.
|
 |
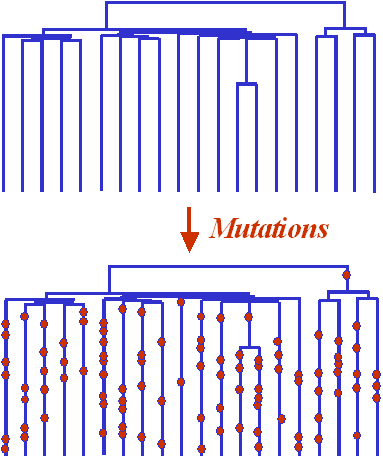 |
La généalogie d'une population ayant connu une
expansion récente sera donc typiquement en forme de
peigne, avec de longues branches terminales et
de courtes branches internes.
Comme les mutations se produisent au hasard le
long des branches de l'arbre, elles auront plus de
chances de survenir sur les branches longues que sur
les branches courtes. Il s'ensuit que la majorité
des mutations vont se produire après l'expansion,
lorsque l'effectif de la population est grand, et
l'on va observer très peu de mutations qui se
sont produites avant l'expansion
|
Distribution du nombre de différences par apires
(distribution mismatch).
Le fait que les mutations se produisent sur les longues
branches de l'arbre et que ces longues branches aient à peu
près toutes la même longueur a une conséquence sur la
diversité moléculaire observée. Lorsque l'on ompare deux à
deux tous les gènes d'une population, ils vont présenter à peu
près le même nombre de différences. Ceci est du au fait que
les temps de coalescences de toutes les paires de l'échantillons
sont très corrélées, et datent d'une brève période
précédant l'expansion.
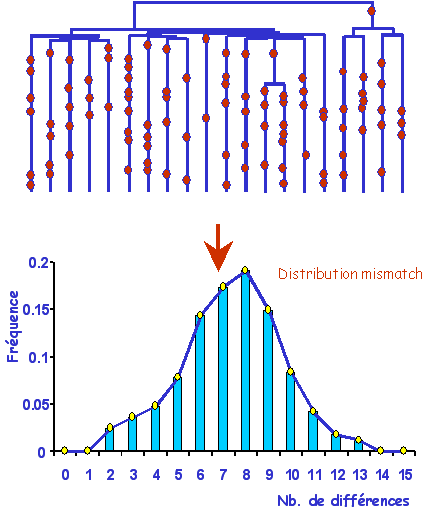
| La forme
caractéristique d'une distribution mismatch dans
population qui a connu une expansion récente sera donc
une courbe en cloche. |
 |
Le mode de la distribution est un indicateur du temps de
l'expansion. En effet, si on a eu une expansion importante il y a
t générations, le temps de coalescence moyen de deux
gènes tirés au hasard sera d'un peu plus de t
générations. Ces deux gènes auront donc été séparés par
environ 2t générations. Si l'on a un taux de mutation u
par génération, alors ces deuc gènes devraient présenter en
moyenne t = 2tu mutations. Il
en découle que
- Le mode de la distribution nous donne une idée
approximative du temps de l'expansion
- Ce temps d'expansion est exprimé en unité de 2u
générations.
- Si l'effectif de la population avant le bottleneck était
déjà assez importante, les temps de coalescence entre
paires de liganges seront moins corrélés et la
distribution sera plus dispersée. L'estimation du temps
de l'expansion sera plsu imprécise.
La distribution mismatch attendue après une expansion
instantanée a été dérivée par Li 1977 et redérivée par
Rogers et Harpending en 1992, sous le modèle des sites infinis.
La probabilité d'observer S différences va dépendre du
temps de l'expansion et de l'effectif de la population avant et
après l'expansion, ces paramètres étant exprimés en unités de
2u générations, et donc égaux respectivement à t = 2tu, q0
= 2N0u , et q1
= 2N1u. Elle dépend est donnée
par
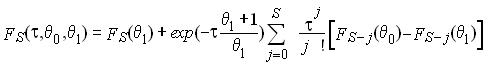
où FS (q)
est la probabilité que deux gènes présentent S
mutations dans une population stationnaire de taille q. et qui a été donnée par watterson
(1975) comme
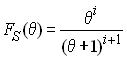
Il semble donc possible d'estimer ces paramètres d'expansion
démographique à partir de la distribution mismatch observée
dans une population, par exemple par la méthode des moindres
carrés, encherchant les paramètres qui minimisent l'écart
entre les points de la distribution mismatch observée et
attendue.
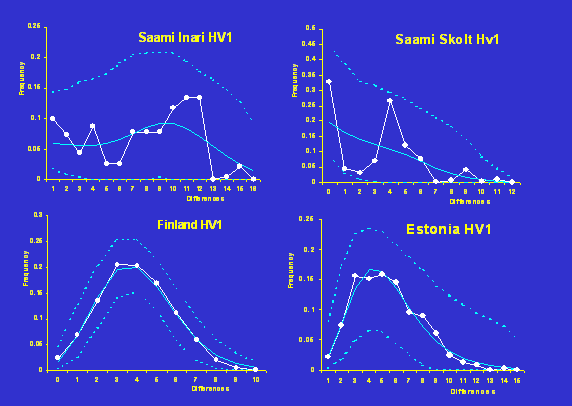
Exemples de distributions mismatch observées pour la région
HV1 de l'ADN mitochondrial humain.
Distribution
mismatch dans des populations européennes
|
 |
Distribution
mismatch dans des populations africaines
|
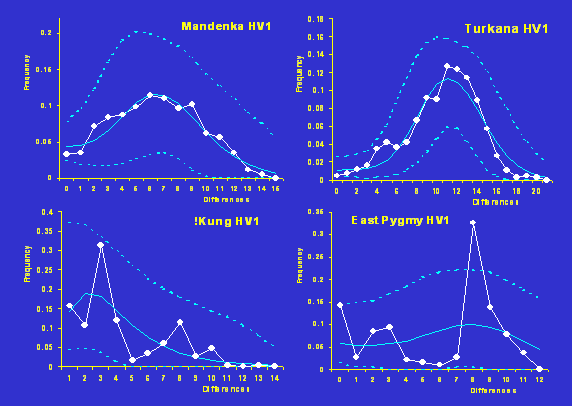 |
Temps
d'expansions relatif estimés pour diverses populations
humaines
|
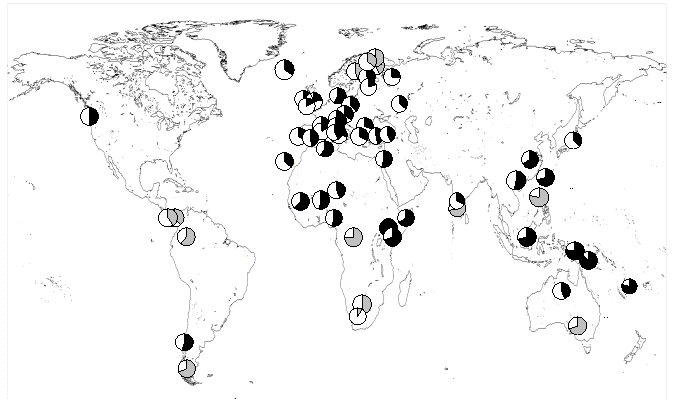 Seuls les
secteurs noirs représentent des expansions
significatives
|
La référence est la population Turkana du nord Kenya, pour
laquelle la date d'expansion la plus ancienne a été trouvée (t=2tu=0.036). Il existe une
polémique importante sur le taux réel de mutation de l'ADN
mitochondrial humain. Les estimations varient de 7% de
différence par million d'années de divergence à plusde 150%.
Nos propres estimations donnent des chiffres d'environ 7%, ce qui
daterait l'expansion démographique des
Turkana à environ 500'000 ans, avec un intervalle de
confiance à 95% de 332'000 à 627'000 ans. Des taux de mutations
plus élevés donneraient des temps d'expansion plus récents.
Toutefois, les dates d'expansion humaines semblent indiquer
qu'elles ont connu pour la plupart une forte expansion
démographique au Pléistocène, et pas au Néolithique.
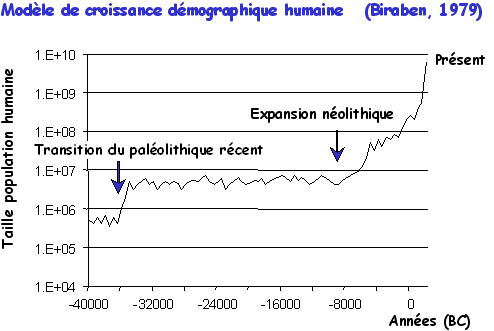
Bien que les démographes et les archéologistes nous disent
que la population humaine a connu une forte expansion au
Néolithique, celle-ci n'aurait pas laissé de trace au niveau
moléculaire, car l'effectif de la population humaine était
déjà trop important avent cette expansion. On voit donc
uniquement la trace d'une expansion qui fait passer une
population d'une très petite taille à une grande taille, et les
expansions ultérieures sont plus difficiles à déceler.
- Calcul de l'effectif de la population néanderthalienne à
partir de la diversité moléculaire de l'ADN
mitochondrial.
- Simuler des expansions de population au moyen de l'applet
TREETOY sur le web. Observer la forme des généalogies
par rapport à une population stationnaire.
- Simulation d'une population stationnaire avec le logiciel
SIMCOAL. Analyse de la distribution de différents
estimateurs du paramètre de mutation q
avec le logiciel Arlequin. Visualisation des
généalogies générées pas SIMCOAL dans le logiciel
TREEVIEW.
Ce TP est accessible sur gmdp_tp4.htm
Laurent Excoffier
: Dernier update : mardi, 30 mai 2006 11:18