| Cours I | Cours II | Cours III | Cours IV | Cours V | Cours VI |
|
Introduction |
Fréquences alléliques Dérive génétique |
Introduction à la coalescence |
Changements démographiques |
Populations subdivisées |
Sélection Tests de neutralité |
| TP I | TP II | TP III | TP IV | TP V | TP VI |
Cours III |
Introduction à la théorie de la coalescence |
L'approche classique de la génétique des populations consiste à essayer de prédire l'évolution du polymorphisme génétique dans une population sous l'influence de différentes forces évolutives. C'est donc une approche essentiellement prospective. Une fois que l'on a compris ce qui se passe au niveau de la population, il faut encore développer la théorie qui concerne des échantillons tirés de la population, car c'est le matériel que l'on observe. D'autre part, la plupart des résultats obtenus font l'hypothèse que la population que l'on considère est à un état d'équilibre entre différentes forces évolutives, par exemple entre la mutation et la dérive génétique, ou entre sélection et dérive.
Ainsi par exemple on va obtenir, après bien des efforts que le nombre de sites polymorphes S attendus dans un échantillon de taille n est égal à (Watterson 1975)
Ce résultats est important et permet d'obtenir une estimation relativement bonne du paramètre q=4Nu.
La théorie de la coalescence a une approche entièrement différente. Elle part d'un échantillon de gènes observés, et vise à reconstruire l'histoire généalogique de ces gènes, selon une certaine histoire démographique de la population et un certain modèle de mutation, jusqu'à l'ancêtre commun le plus récent de ces gènes. On n'a pas donc pas besoin de modéliser l'ensemble de la population. On se préoccupe uniquement de notre échantillon. C'est une approche essentiellement rétrospective.
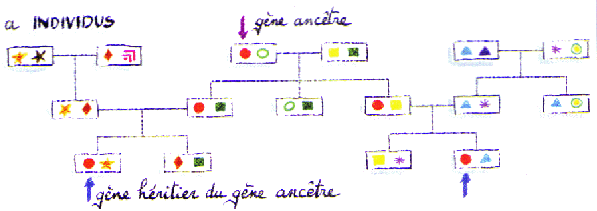
Considérons tout d'abord une généalogie d'individus diploïdes. Chacun de ces individus va avoir un certain nombre de descendants auxquels il aura transmis une des 2 copies de ses gènes à un locus donné. Certains gènes d'un individu ne seront pas transmis, mais d'autres pourront être transmis en un ou plusieurs exemplaires.
 |
Génération 1 |
| Génération 2 | |
| Génération 3 |
Le gène représenté par le rond rouge (gène ancêtre de la génération 1) va être transmis à deux enfants différents à la génération 2, et ces enfants le transmettrons eux-mêmes à un de leur descendants à la génération 3. Ces 2 gènes rouges seront donc identiques par ascendance, et ils auront un ancêtre commun 2 générations auparavant.
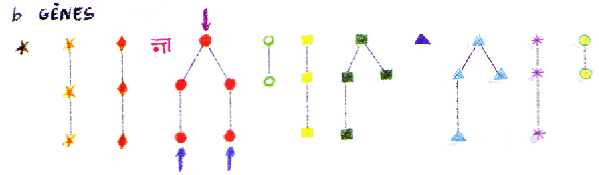
En première approximation on va ignorer le fait que ces gènes se trouvent dans des individus diploides. Cela revient à dire assimiler notre population diploide de taille N à une population haploide de taille 2N. On va ainsi visualiser plus simplement leurs relations d'une génération à l'autre en représentant uniquement les lignes d'ascendance de ces gènes, ou dit plus simplement les lignages de ces gènes. Lorsque deux lignages se rejoignent chez un gêne ancestral, on dit qu'ils coalescent. Il s'agit donc d'un évènement de coalescence.
La théorie de la coalescence décrit donc simplement le processus de coalescence des gènes d'un échantillon depuis la génération présente jusqu'à l'ancêtre commun de tous les gènes d'un échantillon.
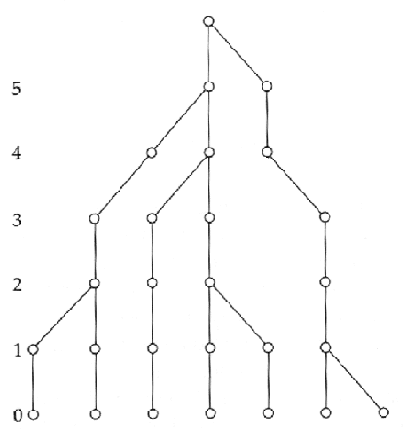
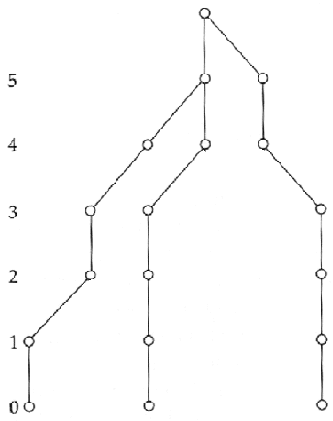
Pour simplifier, considérons une très petite population de taille constante contenant 7 gènes (marqués en bleu) de la figure suivante.
En remontant dans le passé, on voit que les lignages vont progressivement fusionner les uns avec les autres par une série de coalescence (marqués en rouge), jusqu'à un seul ancêtre commun, à la génération 6.
Donc tous les gènes de la générations 0 ont un ancêtre commun 6 générations auparavant. Maintenant, si l'on regarde le processus dans le sens du temps, on voit que un des gènes de la génération 6 s'est fixé dans la population à la génération 0. Les autres gènes de la génération 0 se sont perdus, ils n'ont pas été transmis jusqu'à la génération présente. Ce processus de fixation d'un gène et de perte des autres gènes est en fait exactement le processus de dérive génétique. On voit donc que le processus rétrospectif de coalescence est entièrement analogue à un processus prospectif de dérive génétique. Mais il deux avantages principaux par rapport au processus de dérive.
|
 |
|
 |
Kingman a formellement décrit le processus de coalescence en 1982 pour un échantillon de taille n tiré d'une population diploide de taille N (ou d'une population haploide de taille 2N). Il s'agit d'une marche aléatoire dans le passé ou l'on va passer par des états successifs avec n lignages, n-1, lignages, n-2 lignages etc, jusqu'à l'ancêtre commun où l'on n'aura plus qu'un seul lignage. Bien entendu, le passage d'un état avec j lignages à un état avec j-1 lignages correspond à un évènement de coalescence. Au cours du processus de coalescence, on va donc séjourner pendant un certain temps Tn à un état avec n lignages, puis un temps Tn-1 à un état avec n-1 lignages, etc, pour finir par un temps T2 pendant lequel on n'aura plus que 2 lignages avant l'ultime évènement de coalescence.
Kingman a dérivé la distribution de probabilité de ces temps Tj en faisant les hypothèses suivantes:
Le modèle démographique sous-jacent correspond au
modèle de Wright-Fisher.
La taille de l'échantillon est beaucoup plus petit que la
taille de la population (n<<N), de telle sorte qu'il ne peut y
avoir qu'un seul évènement de coalescence par génération.
On peut dériver ces temps en commençant par s'intéresser à la probabilité d'un évènement de coalescence entre j lignages P(j) à la génération précédente. Si l'on considère une paire de lignages quelconque, c'est la probabilité que ces 2 lignages sont dérivés d'une même copie d'un individu de la génération précédente, c'est à dire qu'ils sont identiques par ascendance à la génération précédente. On a vu que cette probabilité était égale à 1/(2N). maintenant, on doit considérer qu'un lignage peut coalescer avec n'importe quel autre lignage, et ceci avec la même probabilité. Si l'on a j lignages, on peut former j(j-1)/2 paires différentes, ce qui représente le nombre de combinaisons possibles de 2 lignages parmi j. Donc P(j) s'obtient comme
et donc la probabilité qu'il n'y ait aucun évènement de coalescence est 1-P(j). A chaque génération on peut associer une épreuve qui consistera à vérifier s'il y a eu un évènement de coalescence ou non. Le temps de coalescence Tj peut être considéré comme le nombre de générations écoulées jusqu'à ce que l'on ait un évènement de coalescence. C'est donc une variable aléatoire qui est le nombre d'épreuves nécessaires pour observer un succès de probabilité P(j). Une telle variable aléatoire suit une loi géométrique qui a la distribution de probabilité suivante:
Cela revient simplement à dire que pendant t-1 générations il n'y a pas eu de coalescence et qu'il y en a eu une à la t-ième. L'espérance et la variance d'une telle loi géométrique sont connues et égales à
Approximation continue
Comme on fait l'hypothèse que la taille de la populations est grande, on peut considérer que la longueur d'une génération est presque négligeable par rapport à la longueur totale de la généalogie. Dans ce cas, on peut utiliser la version continue de la loi géométrique qui est la loi exponentielle qui a comme densité de probabilité
Cela n'a pas d'effet sur l'espérance, mais la variance des temps de coalescence est simplifié. L'espérance s'obtient comme
et la variance est donnée par
Standardisation
On peut aussi, faire abstraction de la taille de la population en exprimant les temps de coalescence en unité de 2N générations. Dans ce cas, on a simpement
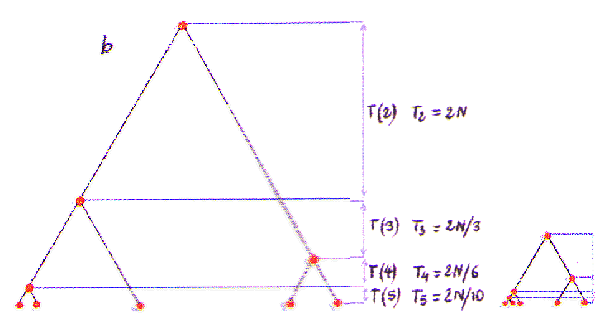
| On peut visualiser l'espérance des temps de coalescence sur une généalogie "moyenne" ou les temps de coalescence seraient égaux à leur moyenne. |
|
|
On remarque que les temps de coalescence moyens augmentent exponentiellement lorsque l'on remonte dans le passé. Donc dans une population stationnaire (de taille constante) on s'attend à ce que la majorité des évènements de coalescence surviennent relativement tôt et que les derniers soient très espacés. Notamment le temps moyen pour la dernière coalescence est égal à 2N générations, avec toutefois une variance égale à 2N(2N-1), soit près du carré de la moyenne. Le processus généalogique a donc une très forte variabilité. Ceci implique que les généalogies de locus indépendants pourront être très différentes. Cette variabilité peut être visualisée et étudiée empiriquement à partir de cette page. Par exemple on peut représenter les généalogies tirés de 6 échantillons de 5 gènes simulés pour la même population stationnaire, mais pour 6 locus différents.
 |
La variabilité des topologies est facilement perceptible, mais notez aussi les différence d'échelle entre les 4 généalogies, ce qui indique aussi des différences considérables de la taille de ces généalogies.
On peut également dériver la taille totale Tn de la généalogie, c'est à dire le temps jusqu'à l'ancêtre commun le plus récent (MRCA en anglais) de tout l'échantillon. On a bien évidement
Lorsque n est grand, on a donc Tn » 4N , ce qui correspond au temps moyen de fixation d'un nouveau mutant de fréquence initiale 1/(2N) dans une population, un résultat bien connu de la génétique des populations prospective. On voit donc de nouveau la relation entre processus de dérive et processus de coalescence.
On notera aussi que comme la probabilité de coalescence de n'importe quelle paire de lignage est identique, toutes les topologies de généalogies ayant les mêmes temps de coalescence sont équiprobables. Ainsi, la topologie b de la généalogie moyenne ci-dessous est aussi probable que la topologie a de la généalogie que l'on a vu ci-dessus.
 |
|
|
Généalogie nucléaire |
Généalogie mitochondriale |
Enfin, il est important de constater que la taille absolue des généalogies va dépendre étroitement de l'effectif efficace de la population d'où elles sont issues. Sur la figure ci-dessus, on a représenté côte à côte la généalogie moyenne d'un gène nucléaire pour lequel il existe donc 2N copies dans la population et la généalogie moyenne d'un gène mitochondrial, pour lequel il existe N/2 copies dans la population, car ils'agit d'un système haploide transmis uniquement par les femmes. On s'attend donc à ce que le TMRCA mitochondrial soit beaucoup 4c fois plus récent que le TMRCA nucléaire, et c'est à peu près ce que l'on remarque par exemple chez l'homme, comme le montre la table ci-dessous..
Etude T MRCA Référence ADN mitochondrial 160-250'000 ans Vigilant et al. 1991 Chromosome Y 170-200'000 ans Hammer, 1995; Tavaré et al. 1997
Chromosome Y 120-150'000 ans Hammer et al. 1998 b-globine 800'000 ans Harding et al. 1997 Chromosome X >200'000 ans Zietkewicz et al. 1998 Chromosome X 1'860'000 ans Harris et Hey 1999 Chromosome X 535'000 ans Koessmann et al. 1999
Jusqu'à présent, nous n'avons pas parlé de mutations, car pour des gènes neutres, le processus de coalescence ne dépend pas du processus de mutation. On peut les considérer comme totalement indépendants. Donc la longueur des branches d'une généalogie dépendra uniquement du processus démographique et pas du processus mutationnel.
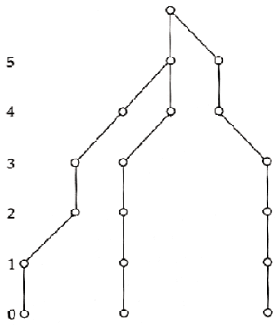
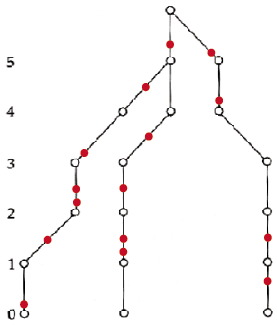
L'addition de mutations au processus de coalescence s'effectue donc d'une manière très simple. On suppose que, pour une généalogie donnée, les mutations se produisent aléatoirement le long des branches.
| Généalogie sans mutation | Généalogie avec mutations |
|---|---|
 |
 |
On fait d'habitude l'hypothèse que les mutations se produisent suivant une loi de Poisson de paramètre l = ut, où u est le taux de mutation par unité de temps, et t la longueur d'un segment de branche quelconque. Dans la version continue du processus de coalescence, où le temps est mesuré en unité de 2N générations, le paramètre l devient
Il convient de bien définir le modèle de mutation que l'on considère. Selon le modèle que l'on va utiliser,le processus de mutation aura différents effets sur la diversité moléculaire observée. Le modèle de mutation le plus simple est le modèle dit des sites infinis a été introduit par Kimura en 1968. Il est en fait l'équivalent du modèle des allèles infinis pour les données moléculaires. Selon ce modèle, toute nouvelle mutation se produit à un nouveau site qui n'a encore jamais été touché par une mutation. Les molécules qui suivent ce modèle ne connaissent donc pas d'homoplasie.
C'est généralement le modèle utilisé pour dériver la plupart des résultats théoriques concernant la variabilité moléculaire des séquences d'ADN. Si la séquence d'ADN considérée est très long et que le taux de mutation est bas, ce modèle constitue une très bonne approximation de la réalité. Il sera donc aproprié pour des molécules d'ADN nucléaire, mais pas très réaliste pour des molécules d'ADN mitochondrial.
Selon ce modèle, la théorie de la coalescence avec mutation peut ainsi tout de suite nous permettre de dériver quelques résultats importants
Sous le modèle des sites infinis, le nombre de sites polymorphes S d'un échantillon est simplement le nombre de mutations s'étant produites dans la généalogie des gènes de l'échantillon. L'espèrance de cette variable aléatoire est simplement fonction de la longueur totale de la généalogie T et du taux de mutation u.
ce qui a été obtenu de manière sensiblement plus compliquée par Watterson en 1975. Un relativement bon estimateur de q basé sur le nombre observé de sites polymorphes est donc obtenu comme
L'homozygotie attendue F est la probabilité que lorsque l'on tire 2 gènes (habituellement chez le même individu), ils soient du même type allélique. Bien évidemment, deux copies d'un gène appartiendront à la même classe allélique (seront une copie du même type allèlique) s'ils ne diffèrent l'un de l'autre par aucune mutation. Donc deux gènes seront donc du même type allélique s'il n'y a pas eu de mutation depuis leur ancêtre commun le plus récent. Cela est donc équivalent à la probabilité d'observer 0 sites polymorphes entre 2 gènes tirés au hasard.
Pour un temps de coalescence donné, la probabilité d'observer zéro mutations entre 2 gènes est égale à
car 2 gènes qui coalescent il y a T2 générations ont été séparés pendant 2T2 générations. On obtient la probabilité non conditionnelle par rapport à T2 en tenant compte de tous les temps de coalescence possibles pour T2 sous l'approximation continue comme
L'homozygotie attendue F est donc donnée par
et l'hétérozygotie attendue H par
On réalise que sous ce modèle l'homozygotie attendue F est égale au coefficient de consanguinité f , puisque obligatoirement 2 gènes du même type allélique sont identiques par ascendance.
Ce TP est accessible sur gmdp_tp2.htm
Laurent Excoffier : Dernier update : mardi, 30 mai 2006 11:15