| Cours I | Cours II | Cours III | Cours IV | Cours V | Cours VI |
|
Introduction |
Fréquences alléliques Dérive génétique |
Introduction à la coalescence |
Changements démographiques |
Populations subdivisées |
Sélection Tests de neutralité |
| TP I | TP II | TP III | TP IV | TP V | TP VI |
Cours II |
Evolution des fréquences alléliques - Dérive génétique |
En absence de forces évolutives telles que la sélection, les mutations ou la dérive génétique, les fréquences génotypiques dépendent uniquement des fréquences alléliques si les individus choisissent aléatoirement leur conjoint pour s'accoupler. Cette union aléatoire des individus implique aussi une union aléatoire de leurs gamètes.
Ainsi, pour un individu diploide, la fréquence attendue du génotype formé des allèles Ai et Aj ayant comme fréquences respectives pi et pj sera de
Si les fréquences attendues des génotypes sont en accord avec les fréquences observées, alors on dira que la population est en équilibre de Hardy-Weinberg, du nom du mathématicien anglais Hardy et du médecin allemand Weinberg qui ont découvert indépendemment cette relation en 1908 (voir la partie du cours évolution pour plus de détails sur cette dérivation).
S'il y a un trop grand écart entre les fréquences attendues et observées, alors on est en droit de penser qu'une force évolutive, comme la sélection, est en jeu, ou encore que les gamètes de la population ne s'unissent pas au hasard. Mais encore faut-il démontrer que cet écart est significatif, c'est à dire plus grand que ce que l'on attendrait par hasard.
Test de Chi-2
La manière classique de comparer des fréquences observées et attendues se fait par un test de Chi-2. Supposons que l'on ait n individus diploïdes dans un échantillon et que l'on observed k allèles à un locus donné. On aura donc potentiellement k(k+1) /2 génotypes différents. Supposons ici que k=3, et que l'on observe les fréquences génotypiques absolues suivantes
A1 A2 A3 A1 n11 n1 A2 n21 n22 n2 A3 n31 n32 n33 n3 n1 n2 n3 n
Classiquement, le test de Chi-2 consiste à comparer les nombres observés des différents génotypes aux nombres attendus sous l'hypothèse de Hardy-Weinberg, soit
A1 A2 A3 A1 n1 A2 n2 A3 n3 n1 n2 n3 n
On calculera donc la statistique
qui devrait suivre asymptotiquement une loi de Chi-2 à k(k-1) /2 degrés de liberté. On déclarera qu'il y aura un écart significatif à l'équilibre de HW si la probabilité associée au X2 est inférieur à un certain niveau de confiance alpha prédeterminé, par exemple alpha=0.05.
Vous pouvez vous exercer à calculer la valeur du X2 sur cette page web et obtenir sa probabilité associée sur celle-ci.
Test exact
Guo et Thompson (1992) ont introduit un test de déséquilibre de HW qui est une extension du test exact de Fisher sur les tables de contingences 2 par 2. Le test exact de Fisher consiste à:
avec H qui est le nombre d'individus hétérozygotes. La probabilité des autres tables s'obtient en changeant la valeur des nij, les ni ne changeant pas car ce sont précisément les sommes marginales.
Pour des petites tables de contingence il est possible d'énumerer de façon exhaustive toutes les tables possibles, mais cela devient fastidieux et trop long pour de grandes tables de contingences (grands échantillons et nombre élevé d'allèles et de génotypes). Dans ce cas on n'explore pas toutes les tables possibles mais un grand nombre au moyen d'une chaîne de Markov. On arrive ainsi à une très bonne approximation de la probabilité exacte dans un temps raisonnables qui ne dépend pas de la taille de la table. C'est cette procédure qui est implémentée dans le logiciel Arlequin (voir section "Methodological outlines" pour plus de détails).
Pour de grands échantillons, l'approximation de Chi-2 est souvent très bonne, mais on préférera un test exact lorsque l'on a de petits échantillons avec de faibles fréquences génotypiques attendues < 5.
Dérivation de la formule de Levene
Il est assez informatif de dériver la formule de Levene. Faisons pour le cas simple d'un locus à 2 allèles A et a, où l'on a donc les fréquences génotypiques suivantes dans un échantillon de n individus.
Génotypes AA Aa aa Fréquences nAA nAa naa
Dans la population, les allèles A et a ont des fréquences (inconnues) de pA et et 1- pA. Sous l'hypothèse de HWE, la probabilité d'observer ces fréquences génotypiques suit une loi multinomiale
.
Les fréquences alléliques inconnues de la population sont un problème, mais on peut s'en débarrasser en calculant la probabilité des fréquences génotypique conditionnelle aux fréquences alléliques observées nA et na. Ces fréquences alléliques ont elles-même une probabilité qui suit une loi binomiale
si bien que la probabilité conditionnelle devient
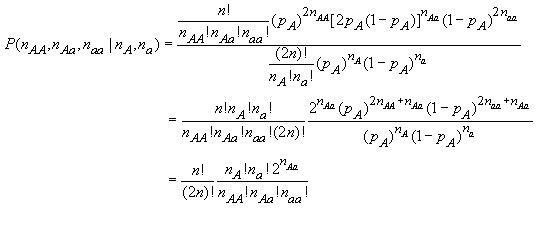
ce qui montre bien que cette probabilité conditionnelle est indépendante des fréquences alléliques dans la population.
Il y a plusieurs raison pour lesquelles on peut rejetter l'hypothèse de HWE. cela peut être du au fait qu'un génotype donné aura une fréquence observée très différente de l'attendue, auquel cas on pourra penser à un phénomène de sélection qui touche ce génotype. Au contraire, le déséquilibre de HW peut toucher l'ensemble des génotypes, ce qui laisse penser à un problème qui touche le système de reproduction, empêchant une union aléatoire des gamètes et des individus. Une telle situation est courante en cas de consanguinité.
Une population est dite consanguine lorsqu'une ceraine proportion d'individus apparentés s'unissent pour produire des descendants dans la population. Dans ce cas, ces descendants de couples consanguins pourront avoir des copies alléliques issues de la même copie d'un de leur ancêtre commun. De ce fait, ils seront donc forcément homozygotes, mais pour une raison indépendante des fréquences alléliques dans la population.
Un marriage entre frère et soeur peut résulter en un individu homozygote avec 2 gènes identiques par ascendance
On s'attend donc intuitivement à ce qu'il y ait un excès d'homozygotes par rapport à HWE dans une population consanguine. Cet excès sera d'autant plus grand qu'il y a d'individus qui possèdent des gènes identiques par ascendance dans la population. Wright (1943, 1951) a proposé d'appeller cette proportion d'individus le coefficient de consanguinité de la population et il est généralement noté f. Cette proportion f correspond donc, pour un individu pris au hasard dans la population, à la probabilité que ses deux copies alléliques soient identiques par ascendance. La consanguinité de la population ne provoque pas de modification des fréquences alléliques au cours du temps, mais elle va affecter les fréquences génotypiques uniquement.
Plus formellement, considérons un locus à deux allèles A et a, de fréquences p et 1-p dans une population diploide de taille supposée infinie. Notons P comme étant la fréquence des homozygotes AA, H celle des hétérozygotes Aa et Q celle des homozygotes aa. On va d'abord chercher à déterminer la fréquences des homozygotes AA. On peut être homozygote de deux manières, soit parce que l'on a deux copies de gènes identiques par ascendance, avec la probabilité f, soit car on a hérité de deux allèles de même type mais indépendants de deux parents non-apparentés, et ceci avec une probabilité 1-f. Donc,
On peut raisonner exactement de la même manière pour les homozygote aa et l'on aura donc
Pour les hétérozygotes Aa, le raisonnement est similaire. Il faut juste réaliser que l'on ne peut être hétérozygote que si ses 2 copies ne sont pas identiques par ascendance et donc
On a donc bien un déficit d'hétérozygotes en cas de consanguinité. On peut donc exprimer f en fonction de ce déficit d'hétérozygotes. En réarrangeant la dernière équation, on obtient
ce qui montre que le coefficient de consanguinité f est égal à 1 moins le rapport de l'hétérozygotie observée sur l'hétérozygotie attendue sous l'hypothèse de HWE.
On peut bien sûr dériver les fréquences attendues des différents génotypes pour plus de 2 allèles, et l'on a, d'une manière générale
On a dit que les fréquences alléliques ne sont pas affectées par la consaguinité. On peut le vérifier en exprimant p en fonction de P, et H. Ainsi
On peut consulter le cours d'évolution sur la consanguinité pour visualiser l'effet du coefficient f sur les fréquences génotypiques.
Consanguinité et corrélation des gamètes
Wright a aussi montré que le coefficient de consanguinité f était égal à la corrélation des deux gamètes d'un individu par rapport à deux gamètes pris au hasard. Voyons cela de plus près et considérons une population où l'on a 2 allèles A et a de fréquence p et 1-p. On a une certaine proportion d'hétérozygotes Ho dans cette population. On voit dans la table qui suit que l'on peut exprimer les fréquences génotypiques dans la population en fonction de la fréquences des hétérozygotes Ho et des fréquences alléliques, sans faire l'hypothèse de HWE.
Fréquences des différents génotypes dans la population
Gamète 2
A
a
Total
Gamète 1
A
p
a
1-p
Total p
1-p
1
On va considérer une variable indicatrice y qui sera égale à 1 si on tire un gamète de type allélique A et à 0 si on tire un a. On voit tout de suite que si l'on répète l'épreuve qui consiste à tirer un grand nombre de gamète, l'espérance de y est égale à
E(y) = p.1 + (1-p) .0 = p
De la même manière, E(y2) = p et la variance de y est obtenue facilement comme
Pour calculer la corrélation de deux gamètes y1 et y2, il ne nous manque plus que leur covariance cov(y1, y2). Celle-ci est obtenue de manière standard comme
cov(y1, y2) = E(y1y2) - E(y1) E( y2)
La simple consultation de la table précédante nous permet d'obtenir facilement cette covariance, car il apparaît que
Ainsi,
et
On remarque donc que la corrélation de deux gamètes est bien égale à f, le coefficient de consanguinité défini un peu plus haut.
La notion de corrélation entre gamètes est intimement liée aux statistiques- F (F-statistics) définies par Wright (1943, 1951) dans le cas de populations subdivisées. Nous y reviendrons par la suite, mais il est important de noter ici que le coefficient de consanguinité est équivalent à la statistique FIS définie par Wright comme la corrélation moyenne des 2 gènes d'un individu par rapport à deux gènes pris au hasard dans une des subdivisions de la population.
Finalement on notera que d'autres systèmes de reproduction causent des écarts à l'HWE, comme l'autofécondation totale ou partielle, ou le choix du conjoint sur la base de son phénotype (assortative mating).
Alors que dans des populations de taille infinie les fréquences alléliques sont stables au cours des générations en l'absence de sélection et de mutation, les fréquences alléliques varient aléatoirement dans des populations de taille finie. Cela est du à la variabilité du tirage aléatoire des gènes d'une génération à l'autre.
Pour permettre un traitement mathématique pas trop compliqué, on modélise la transmission des gènes d'une génération à l'autre de façon très schématique. Ce modèle est une simplification considérable du cycle de reproduction des populations naturelles. Il représente à peuprès celui d'une population monoèce pratiquant l'autofécondation, mais avec des générations séparées. Dans ce cas, une population de N individus peut êre représentée par un vecteur de 2N copies alléliques.
Tansmission aléatoire avec répétition des gamètes entre générations séparées 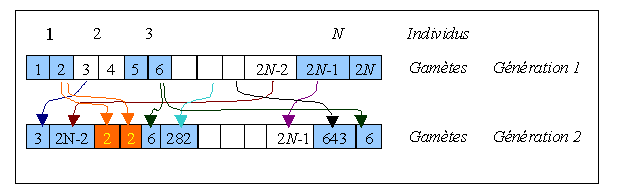
Selon ce modèle, les 2N gènes des individus d'une certaine génération sont tirés avec répétition à partir des 2N gamètes de la génération précédente. Le nombre de copies transmises d'un certain gamète suit donc une loi de Poisson de paramètre l=1.
Conséquences:
Intéressons nous de nouveau à un locus à 2 allèle A et a, où la fréquence de l'allèle A est p dans une population diploide de taille N suivant le modèle de Wright-Fisher.Quelle va être la fréquence de l'allèle A à la prochaine génération. Sur la figure précédente on voit que la nouvelle génération est formée par tirage aléatoire de 2N gènes à partir du pool gamétique de la génération précédente.On considère en général que la taille de ce pool gamétique est infini, du fait que chaque individu produit un nombre considérable de gamètes.
La constitution de la nouvelle génération consite donc à répéter 2N épreuves élémentaires où l'on a à chaque fois une probabilité p de tirer un allèle A et une probabilité 1-p de tirer un allèle a. Le nombre X d'allèle A à la prochaine génération est donc une variable aléatoire qui suit donc une loi binomiale de paramète b(2N, p). La probabilité d'observer r allèles est donnée par
et r peut donc varier de 0 à 2N copies, impliquant que p(t+1) peut prendre des valeurs variant entre et comprenant 0 et 1, avec une certaine probabilité donnée par la loi binomiale.
Distribution de probabilité de la fréquence de l'allèle A si la fréquence à la génération prédédente est de p=0.5
Distribution de probabilité de la fréquence de l'allèle A si la fréquence à la génération prédédente est de p=0.1
L'espérance de X est bien sûr donné par E(X) = 2N p, et sa variance par V(X) = 2N p (1-p).
On peut facilement obtenir l'espérance et la variance de p(t+1) comme
Comme cela était déjà clair sur les figures ci-dessus, l'espérance de la fréquence de l'allèle A à la génération t+1 est sa fréquence à la génération t, et donc de sa fréquence initiale p0. Par contre, si l'espérance de la fréquence allélique est constante, sa variance est d'autant plus grande que la population est petite. En d'autres termes, la taille finie de la population provoque une variation aléatoire des fréquences alléliques d'une génération à l'autre. Si l'on part d'une fréquence initiale donnée p0, la fréquence de l'allèle A variera aléatoirement au cours des générations, et ceci d'autant plus que la taille de la population sera petite. On peut visualiser ce processus de dérive génétique sur les figures suivantes.
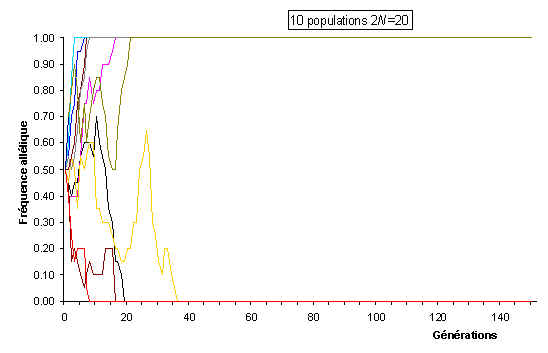
Dans une population de 10 individus diploides, on va fixer rapidement un allèle ou un autre en partant de 0.5. Notez aussi la très grande amplitude des changements de fréquence d'une génération à l'autre.
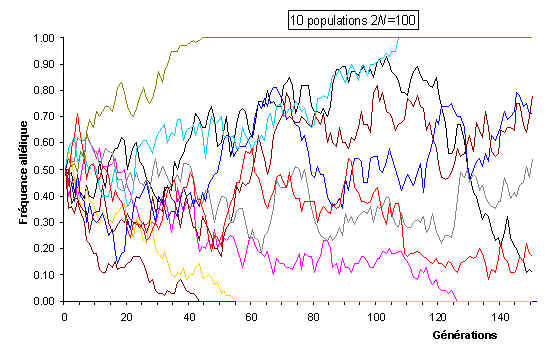
Dans un epopulation de 50 individus, un polymorphisme va pouvoir être maintenu pendant une plus longue période, mais ultimement on aura aussi fixation ou perte d'allèle. Les fréquences alléliques varient toujours fortement d'une génération à l'autre.
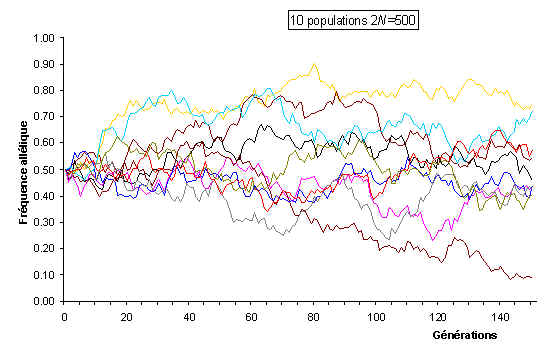
Avec 250 individus, aucune population n'a fixé d'allèles au bout de 150 générations. Les variations de fréquences alléliques sont aussi de plus faible amplitude.
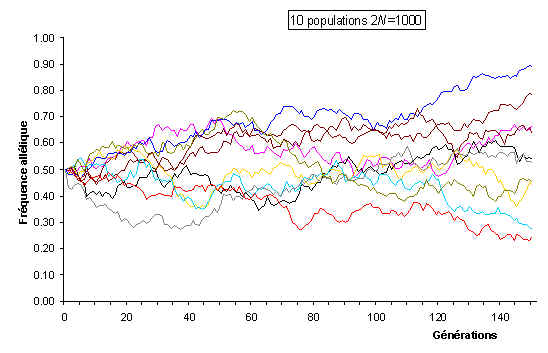
Avec 500 individus, les fréquences varient relativement faiblement autour de la fréquence initiale. On se rend compte que la moyenne des fréquences alléliques tend vers la fréquence initiale.
Vous pouverz aussi aller sur ce site pour essayer d'autres combinaisons de paramètres.
Ces différentes courbes correspondent à des réplications indépendentes du processus d'évolution des fréquences alléliques à partir d'une même fréquence initiale. Cela pourrait correspondre à l'évolution de différents locus dans la même population, ou à l'évolution de différentes populations ayant divergé à partir d'une certaine population ancestrale. Dans ce cas, on se rend compte que la divergence des populations augmente régulièrement au cours du temps.cette divergence est liée à l'augmentation de la variance des fréquences allélique de génération en génération. On peut en effet montrer que l'évolution de la variance au cours du temps est donnée par
Sur la figure suivante, on a représenté, pour différents nombres de gènes dans la population (2N), l'enveloppe p0=0.5 ± s(t).
Cette augmentation régulière de la variance des fréquences alléliques peut être utilisée pour calculer le temps de séparation d'un ensemble de populations (sous l'hypothèse qu'elles n'ont pas échangé de migrants). On suppose qu'on observe un ensemble de populations ayant des fréquences alléliques p1, p2, p3, ... pi, ..., pd. La fréquence moyenne sur l'ensemble des populations va se rapprocher de la fréquence initiale p0 et on peut ré-écrire l'équation précédente comme:
et le temps de divergence exprimé relativement à la taille des populations s'obtient facilement comme
Attention: Pour que ce temps de divergence ait un sens il faut que les hypothèse de notre modèle soient vérifiées. Si il y a des migrations entre les populations ce temps de divergence sera sous-estimé. Si les populations ne sont pas toutes de même taille, il sera sur-estimé. Enfin, notez que comme D dépend inversément de N, un certain degré de divergence sera obtenu beaucoup plus rapidement pour des petites populations que pour des grandes.
Dans le modèle de Wright-Fisher, il est parfaitement possible que les 2 copies alléliques d'un individu soient identiques par ascendance d'une même copie de la génération précédente, et cet évènement à une probabilité égale à 1/(2N). Dans le cas contraire, il est aussi possible que les 2 copies soient identiques par ascendance mais à une génération antérieure. Le coefficient de consaguinité f de la population à la génération t+1 va donc être égal à
La consanguinité de la population va ainsi augmenter au cours du temps du fait de la taille finie de la population. L'hétérozygotie de la population va du même coup diminuer. On a vu plus haut que le coefficient de consanguinité et l'hétérozygotie étaient liés par la relation 1 - f = H / [ 2 p (1 - p) ]. Ainsi, en commançant par ajoutter 1 aux 2 côtés de l'équation précédente, on obtient
en ignorant les modifications de fréquences alléliques dus à la dérive génétique. L'hétérozygotie de la population décline donc à un taux égal à 1/(2N) par génération, et à terme il n'y aura que des homozygotes dans la population du fait du processus de fixation des allèles par dérive génétique. L'hétérozygotie moyenne de la population variera donc au cours du temps selon la relation suivante:
et la consanguinité selon
On a vu que la loi binomiale donnait la probabilité qu'un allèle passe d'une fréquence p à la génération t à la fréquence p' à la génération t+1. Si l'on raisonne en terme de fréquence absolue, on voit que la loi binomiale décrit la probabilité de passer de i copies à j copies en une génération, probabilité que l'on peut noter pij.
On peut ainsi représenter l'évolution des fréquences alléliques dans une population de taille N comme une marche aléatoire dans un espace où les probabilités de déplacement sont définie par une matrice de transition de taille (2N+1) dont les éléments sont précisément les pij. Par exemple, pour une population de 10 individus, on peut visualiser la matrice de transition dans la figure suivante.
Matrice de probabilité de transition entre fréquences alléliques dans une population de 10 individus diploides.
La probabilité de passer d'une certain nombre de copies à un autre
est exprimé sur l'axe Z.
Cette marche aléatoire peut être assimilée à une chaîne de Markov dont les probabilités de transitions entre états {0, 1, 2, 3, ..., i, ... , 2N-2, 2N-1, 2N}sont définis par les probabilités binomiales
Comme les états 0 et 2N sont absorbants, le résultats d'une marche aléatoire dans cette chaîne ne peut qu'aboutir à la perte (i = 0) ou à la fixation (i = 2N) d'un allèle. D'autre part, comme pour toute chaîne de Markov, la probabilité d'effectuer une certaine transition ne dépend que de l'état présent et pas des états antérieurs, et donc pas du chemin déjà parcouru. On peut donc théoriquement prédire l'évolution des fréquences alléliques dans une population de n'importe quelle taille, mais pratiquement cette approche matricielle est limitée à des populations de petites taille.
Pour des populations de grande taille, on approxime cette marche aléatoire dans un espace discret par un processus de diffusion dans un espace continu. Cette approche a été principalement introduite par Kimura.
Dans ce qui a précédé, nous n'avons pas considéré la possibilité d'avoir des mutations qui sont une des forces évolutives. L'apparition de nouveaux mutants va avoir plusieurs conséquences dont la première est de mofifier les fréquences alléliques dans les populations de taille finie, et une autre et d'empêcher la fixation ultime des allèles. Les mutations vont donc interférer quelque peut avec le processus de dérive génétique.
Dans le modèle des allèles infinis, on fait simplement l'hypothèse qu'une mutation provoque l'apparition d'un nouvel allèle qui n'était encore jamais apparu dans la population. La fréquence initiale de ce nouvel allèle sera bien évidemment de
Kimura et Crow (1964) ont montré que la probabilité de fixation d'un nouveau mutant neutre était sa fréquence initiale soit 1/(2N). la probabilité qu'il soit ultimement perdu par dérive génétique est donné par la probabilité complémentaire soit, 1-1/(2N).
Kimura et Ohta (1971) ont dérivé le temps moyen de fixation T1 pour un nouveau mutant neutre comme étant égal à
el le temps moyen de sa perte T0 comme étant
soit un temps beaucoup plus court que sa fixation.
Dans des populations de taille finie et en présence de mutations, de nouveaux allèles vont être introduits par mutation et d'autres seront perdus par dérive. Il peut s'établir un équilibre entre ces 2 forces qui va conditionner le nombre d'allèle qui pourrront être maintenus dans une population de taille donnée.
Nous avons vu plus haut que la taille finie des populations conduisait à une augmentation de la consanguinité de la population. En présence de mutation, cette augmentation de l'homozygotie va être quelque peu freinée par l'introduction de nouveaux allèles. Plus formellement, le changement du coefficient de consanguinité au cours du temps va maintenant être conditioné par le fait que les copies d'un individu ne pourront être identiques par ascendance que si elles n'ont pas muté aucours de la dernière génération. Ainsi
ou u est le taux de mutation par gène par génération. A l'équilibre mutation-érive, f(t+1) = f(t) = f , si bien que
On peut résoudre cette équation pour f pour aboutir à
et si l'on ignore les termes en u2 on obtient
Dans un modèle avec mutation le coefficient de consanguinité à l'équilibre mutation dérive est équivalent à l'homozygotie de la population, puisque deux copies alléliques du même type seront obligatoirement issue d'une même copie sans mutation si l'on remonte suffisamment loin dans le passé.
Crow et Kimura ont défini le nombre efficace d'allèle pouvant être maintenu à l'équilibre mutation-dérive ne comme la réciproque de la consanguinité, soit
Ce nombre est défini ainsi car il correspond au nombre fictif d'allèles ayant tous une fréquence identique et qui donnerait lieu à l'hétérozygotie attendue.
Remarque: On représente souvent la quantité 4Nu par la notation q , qui correspond donc au produit de la taille de la population par le taux de mutation. Ces 2 quantités sont rarement estimables séparément au vu de la diversité génétique de la population et seul q peut être estimé indépendamment.
Ce TP est accessible sur gmdp_tp2.htm
Laurent Excoffier : Dernier update : mardi, 30 mai 2006 11:18